Question

I need help with part C and D and F.

Answer 1

Problem Statement

The question tells us that the number of births for a whole year follows a uniform distribution. We are asked to find the following:

1. The probability that a child is born exact at the beginning of the 18th week.

2. Probability that a child is born between weeks 10 and 43.

3. P(x > 18 | x < 32)

Method

To evaluate the probability of a uniform distribution, we need to know a couple of things:

1. The probability that a child is born in weeks 1, 2, 3, and so on, up to week 53, is equal and the probability is:

`P(1\text{ w}eek)=(1)/(52)`

2. The way to find the probability within a range of weeks is:

To find the probability between the two weeks, m and n, we simply find the area of the rectangle.

`\begin{gathered} The\text{ length of the rectangle is:}Week\text{ n - W}eek\text{ m} \\ \text{width of the rectangle is: }(1)/(52) \\ \\ \text{Thus, the area is: }(n-m)*(1)/(52) \end{gathered}`

With the above information, we can proceed to solve the question.

Implementation

1. The probability that a child is born exact at the beginning of the 18th week.

This means that m = 18 and n = 18. Thus, the probability that a child is born at the beginning of the 18th week is:

`\begin{gathered} (n-m)*(1)/(52) \\ P(\text{exactly 18 w}eeks)=(18-18)*(1)/(52) \\ \\ P(\text{exactly 18 w}eeks)=0 \end{gathered}`

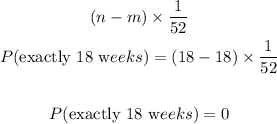
2. Probability that a child is born between weeks 10 and 43.

This means that m = 10 and n = 43. Thus the probability of being born between weeks 10 and 43 is:

`\begin{gathered} P(\text{between 10 and 43)}=(43-10)*(1)/(52) \\ \\ \therefore P(\text{between 10 and 43)}=(33)/(52) \end{gathered}`

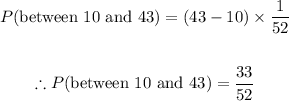
3. P(x > 18 | x < 32)

This is a conditional probability as such, we can apply the Bayes theorem which states:

`\begin{gathered} P(A|B)=(P(A\cap B))/(P(B)) \\ A=\mleft\lbrace x>18\}\mright? \\ B=\mleft\lbrace x<32\}\mright? \\ \\ \therefore P(\mleft\lbrace x>18\mright\rbrace|\mleft\lbrace x<32\mright\rbrace)=(P(\lbrace x>18\rbrace\cap\lbrace x<32\rbrace))/(P(\lbrace x<32\rbrace)) \\ \\ \lbrace x>18\rbrace\cap\lbrace x<32\rbrace\text{ tells us that x is within the range: 18 < x < 32. } \\ \therefore\P(\lbrace x>18\rbrace\cap\lbrace x<32\rbrace)=P(1818\rbrace|\lbrace x<32\rbrace)=(14)/(52)/(31)/(52)=(14)/(52)*(52)/(31) \\ \\ P(\lbrace x>18\rbrace|\lbrace x<32\rbrace)=(14)/(31)\approx0.4516 \end{gathered}`