20% is 20/100 = 0.2
90% is 90/100 = 0.9
Let,
x liters of 20% solution needed
y liters of 90% solution needed
Thus, we can say:
0.2 of x SUM with 0.9 y GIVES up 140 Liters of 50% solution
We can write:
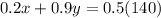
Also, we know we will have a total of 140 liters, so we can say:
x + y = 140
or
y = 140 - x
Now, substituting this into 1st and solving, we get:

We know y = 140 - x, so
y = 140 - 80 = 60
Thus,
x = 80
y = 60
so,
we need 80 liters of 20% solution and 60 liters of 90% solution