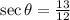Question

Hi, can you help me to solve this exercise please!!

Answer 1

Given that

`\tan \theta=(5)/(12)\text{ and 0}^0<\theta<90^0,`

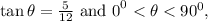
we are asked to find the value of sec θ. This can be seen below.

Step-by-step explanation

`\tan \theta=(5)/(12)=\frac{\text{opposite}}{Adjacent}`

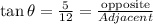
We can represent the information in the diagram below;

Therefore we know that

`\sec \theta=(Hypotenuse)/(Adjacent)`

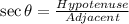
This implies we will need to get the hypotenuse using the Pythagoras theorem. Hence;

`\begin{gathered} (\text{Hypotenuse)}^2=(\text{opposite)}^2+(\text{adjacent)}^2 \\ x^2=12^2+5^2 \\ x=\sqrt[]{144+25} \\ x=\sqrt[]{169} \\ x=13 \end{gathered}`

Therefore,

`\sec \theta=\frac{\text{Hypotenuse}}{Adjacent}=(x)/(12)=(13)/(12)`

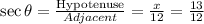
Answer:

`\sec \theta=(13)/(12)`