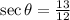Given that
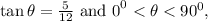
we are asked to find the value of sec θ. This can be seen below.
Step-by-step explanation
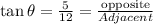
We can represent the information in the diagram below;
Therefore we know that

This implies we will need to get the hypotenuse using the Pythagoras theorem. Hence;
![\begin{gathered} (\text{Hypotenuse)}^2=(\text{opposite)}^2+(\text{adjacent)}^2 \\ x^2=12^2+5^2 \\ x=\sqrt[]{144+25} \\ x=\sqrt[]{169} \\ x=13 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/109eo9jwttw2k1efw69cccokx55j30f8by.png)
Therefore,
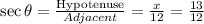
Answer: