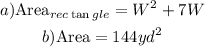
Step-by-step explanation
Step 1
Graph
The length of the fences is 7 more than the width. ,so
Length= Width+7
replacing
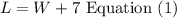
Step 2
a) Write a polynomial that represents the area by the fence.
the area of a rectangle is given by:
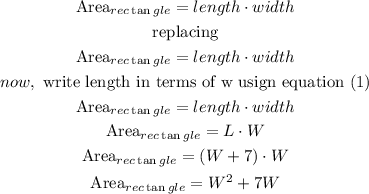
Step 3
b) Find the area when the width is 9 yards.
replace the value of W in the equation of the area.
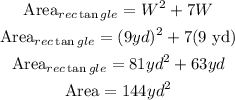
I hope this helps you