SOLUTION
Step1: Write out the formula for test statistic
![t=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt[]{n}}}](https://img.qammunity.org/2023/formulas/mathematics/college/5d56fhj2daei9sxmtg87bymq68nahr3c9p.png)
Step2: Identify the given parameter in the question
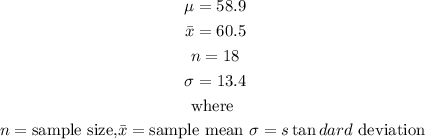
Step3; Substitute the values into the formula
![\begin{gathered} t=\frac{60.5-58.9}{\frac{13.4}{\sqrt[]{18}}} \\ \\ t=(1.6)/((13.4)/(4.24)) \\ \\ t=(1.6)/(3.16) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/zcbvq0vnmzy4dmu3ynp71oelbl07243ylr.png)
Step4: Simplify the expression in the last line above
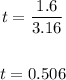
Therefore the test statistics is 0.506 to 3 d.p