Question

I need help answering this practice problem for my calculus prep guide

Answer 1

The Solution:

Given the formula for the nth term of a sequence as below:

`(8n^4-5)/(6n^4+7)`

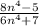
We are required to find the limit of the nth term as n tends to infinity.

`\lim _(n\to\infty)((8n^4-5)/(6n^4+7))`

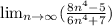
Step 1:

Divide each term by the highest denominator power.

`\lim _(n\to\infty)(\frac{(8n^4)/(n^4)^{}-(5)/(n^4)}{(6n^4)/(n^4)^{}+(7)/(n^4)})=\lim _(n\to\infty)(\frac{8^{}^{}-(5)/(n^4)}{6^{}^{}^{}+(7)/(n^4)})`

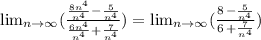
Step 2:

Substitute infinity for n, we have

`(\frac{8^{}-(5)/(\infty^4)}{6^{}+(7)/(\infty^4)})=(\frac{8^{}-0^{}}{6^{}+0^{}})=(8)/(6)=(4)/(3)`

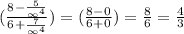
Therefore, the correct answer is 4/3 [option 3]