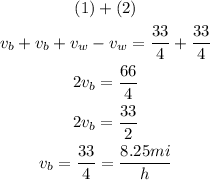Let's use the following formula:
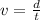
We have two speeds in this case, the speed of the boat and the speed of the water, so:
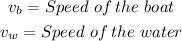
When the boat travels 33 miles downstream in 4 hours, we can say that their speeds add up:
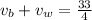
When the boat return, we can say that their speeds are subtracted:
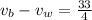
with this we can form a system of equations 2x2:
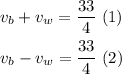
Let's solve for vb: