Question

Determine if the sequence below is arithmetic or geometric and determine the common difference / ratio in simplest form.15,10,5

Answer 1

In a geometric sequence, the ratio between two consecutive terms is constant. Computing this ratio for the given sequence, we get:

`\begin{gathered} r_1=(10)/(15)=(2)/(3) \\ r_2=(5)/(10)=(1)/(2) \end{gathered}`

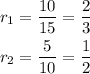
Given that the ratios are different, then the sequence is not geometric.

In an arithmetic sequence, the difference between two consecutive terms is constant. Computing this difference for the given sequence, we get:

`\begin{gathered} d_1=10-15=-5 \\ d_2=5-10=-5 \end{gathered}`

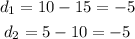
Given that the differences are equal, then the sequence is arithmetic. The common difference is -5.