Question

Question 25 of 25The vertex of the parabola below is at the point (2, 4), and the point (3,6) ison the parabola. What is the equation of the parabola?10(3,6)-10-10-(2,4)10

Answer 1

`B)y=2(x-2)^2+4`

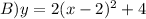
1) Since the vertex is at (2,4) and there is another point, we can write out the following using the vertex quadratic form and those points:

`\begin{gathered} y=a(x-h)^2+k \\ \\ 6=a(3-2)^2+4 \\ \\ 6=a+4 \\ \\ 6-4=a \\ a=2 \end{gathered}`

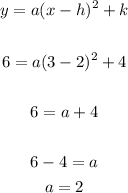
2) Now, that we know the coefficient "a" we can tell that this is the equation of that parabola by plugging a=2 into the vertex form:

`y=2(x-2)^2+4`

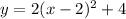
And that is the answer.