We are given the following information
Mean lifetime of a bulb = 600 hours
Standard deviation of the lifetime of a bulb = 20 hours
P(X ≤ 630) = ?
At most 630 hours means equal to or less than 630 hours.
Since the life of light bulbs is normally distributed, we can calculate the probability using the z-score.
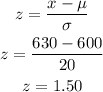
From the z-table, the probability corresponding to the z-score of 1.50 is found to be 0.9332
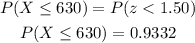
Therefore, the probability of a bulb lasting for at most 630 hours is 0.9332