![\begin{gathered} a)\text{ coordinates of center of circle (h, k) = (-3, 2)} \\ \text{Length of radius is }\sqrt[]{20} \\ \\ b)\text{ }(0,\text{ }2+\text{ }\sqrt[]{11}),\text{ (}0,\text{ }2-\sqrt[]{11}),\text{ (1, 0), (-7, 0)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/javaymeecza01owpiwhlk13l9hsx69l4n2.png)
Step-by-step explanation:
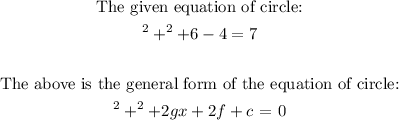
There are different form a circle can be written:
i) the general form (the one with f, g and c)
ii) the standard form that has the vertex (h, k) and radius r
To get the coordinates of the center of circle and the radius, we need to convert to the standard form of circle:
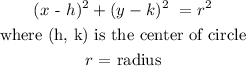
To find f, g and c from the given equation:
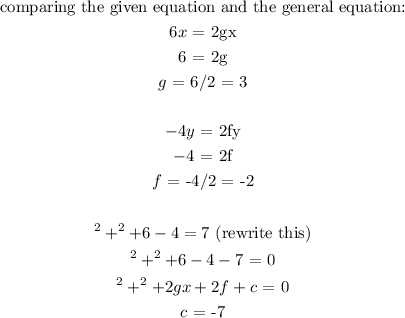
We need to find the center (h, k):

Next, let's find the radius of the circle:
![\begin{gathered} \text{r = }\sqrt[]{g^2+f^2-c} \\ \text{r = }\sqrt[]{3^2+(-2)^2-(-7)} \\ \text{r = }\sqrt[]{9+4+7} \\ r\text{ = }\sqrt[]{20} \\ \\ \text{Length of radius is }\sqrt[]{20} \\ We\text{ will leave the value of the radius in this form as 2}0\text{ isn't a p}\operatorname{erf}ect\text{ square} \end{gathered}]()
The equation in standard:
![\begin{gathered} (x\text{ - (-3)})^2+(y-^{}2)^2\text{ }=(\sqrt[]{20})^2 \\ (x\text{ +3})^2+(y-^{}2)^2\text{ }=20\text{ } \\ \text{The above was not asked in the question but just to know how it will look when all values are inserted)} \end{gathered}]()
b) To find the coordinates where the circle crosses both axes, we will equate the y and x coordinate in the equation of circle to zero respectively:
![\begin{gathered} ^2+^2+6-4=7 \\ \text{when x = 0} \\ (0)^2+y^2\text{ + 6(0) - 4y = 7} \\ 0+y^2\text{ + 6(0) - 4y = 7} \\ y^2\text{ - 4y -7 = 0} \\ u\sin g\text{ quadratic formula:} \\ y\text{ = }\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ a\text{ = 1, b = -4, c = -7} \\ y\text{ = }\frac{-(-4)\pm\sqrt[]{(-4)^2-4(1)(-7)}}{2(1)} \\ y\text{ = }\frac{4\pm\sqrt[]{16+28}}{2}\text{ = }\frac{4\pm\sqrt[]{44}}{2} \\ y\text{ = }\frac{4\pm\sqrt[]{4*11}}{2}\text{ = }\frac{4\pm\text{ 2}\sqrt[]{11}}{2} \\ y\text{ = }\frac{2(2\pm\text{ }\sqrt[]{11})}{2}\text{ = }2\pm\text{ }\sqrt[]{11} \\ y\text{ = }2+\text{ }\sqrt[]{11}\text{ or }2-\sqrt[]{11} \\ \\ In\text{ coordinate form: (x, y)} \\ (0,\text{ }2+\text{ }\sqrt[]{11}),\text{ (}0,\text{ }2-\sqrt[]{11}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f6jo7pvo9xrmdhc1xjwlm22mj3ogchpc3x.png)
when y = 0
![\begin{gathered} ^2+^2+6-4=7 \\ ^2+(0)^2+6-4(0)=7 \\ ^2+0+6-0=7 \\ ^2+6=7 \\ ^2+6-7=\text{ 0} \\ u\sin g\text{ quadratic formula:} \\ x\text{ = }\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{a = 1, b = 6, c = -7} \\ x\text{ = }\frac{-6\pm\sqrt[]{(6)^2-4(1)(-7)}}{2(1)} \\ x\text{ = }\frac{-6\pm\sqrt[]{36+28}}{2}\text{ = }\frac{-6\pm\sqrt[]{64}}{2} \\ x\text{ = }(-6\pm8)/(2) \\ x\text{ = }(-6+8)/(2)\text{ or }(-6-8)/(2) \\ x\text{ = 2/2 or -14/2} \\ x\text{ = 1 or -7} \\ \\ In\text{ coordinate form: (x, y)} \\ (1,\text{ 0) , (-7, 0)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6bptuwlep2ls60vycvhb6fofxmotp8i3uu.png)
![\begin{gathered} \text{Hence, the coordinates of where the circle crosses both axes:} \\ (0,\text{ }2+\text{ }\sqrt[]{11}),\text{ (}0,\text{ }2-\sqrt[]{11}),\text{ (1, 0), (-7, 0)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1fql16xreqvcstl2mt9t3ap92jb0j5w0h4.png)