Answer:
The weight of the contents in the container is;

Step-by-step explanation:
Given that the shipping container is in the shape of a right rectangular prism with a length of 12 feet, a width of 13.5 feet, and a height of 15 feet.
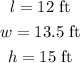
Recall that the volume of a right rectangular prism can be calculated using the formula;

substituting the given values;
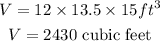
from the question,the container is completely filled with contents that weigh an average, 0.47 pound per cubic foot.
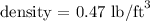
The weight of the content would be;
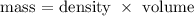
substituting the density and volume of contents, we have;
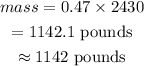
Therefore, the weight of the contents in the container is;
