1 Answer

Mathifonseca · Answer 1 · 2023-10-16T22:38:04+0000

In this multiple choice question, we want to determine which option gives us a solution of (1,6).

The quickest way to do this is to test the point in each equation. We know

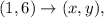
$(1,6)\rightarrow(x,y),$

so we can simply substitute the value of x and y into each set to see if they both make the equations true.

Option A:

We are given the equations:

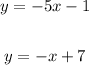
$\begin{gathered} y=-5x-1 \\ \\ y=-x+7 \end{gathered}$

Substituting the point (1,6) into the first equation gives us:

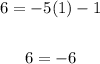
$\begin{gathered} 6=-5(1)-1 \\ \\ 6=-6 \end{gathered}$

This is already a false equation, so Option A is not correct.

Option B:

We have

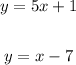
$\begin{gathered} y=5x+1 \\ \\ y=x-7 \end{gathered}$

We will substitute into the first equation:

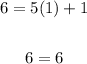
$\begin{gathered} 6=5(1)+1 \\ \\ 6=6 \end{gathered}$

The first equation works. Now, let's try the second equation:

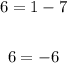
$\begin{gathered} 6=1-7 \\ \\ 6=-6 \end{gathered}$

Unfortunately, that is a false statement, so Option B is not our answer.

Option C:

The equations are

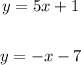
$\begin{gathered} y=5x+1 \\ \\ y=-x-7 \end{gathered}$

From the previous question, we know the first equation is true. For the second equation, we have

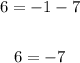
$\begin{gathered} 6=-1-7 \\ \\ 6=-7 \end{gathered}$

This is false.

Option D:

Through process of elimination, this is the correct answer. However, let's prove it.

We know the first equation worked, so let's try the second:

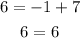
$\begin{gathered} 6=-1+7 \\ 6=6 \end{gathered}$

The correct answer is Option D.

$\begin{gathered} y=5x+1 \\ \\ y=-x+7 \end{gathered}$

Please log in or register to add a comment.