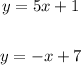In this multiple choice question, we want to determine which option gives us a solution of (1,6).
The quickest way to do this is to test the point in each equation. We know
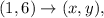
so we can simply substitute the value of x and y into each set to see if they both make the equations true.
Option A:
We are given the equations:
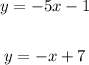
Substituting the point (1,6) into the first equation gives us:
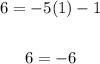
This is already a false equation, so Option A is not correct.
Option B:
We have
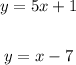
We will substitute into the first equation:
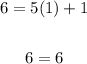
The first equation works. Now, let's try the second equation:
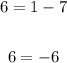
Unfortunately, that is a false statement, so Option B is not our answer.
Option C:
The equations are
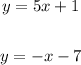
From the previous question, we know the first equation is true. For the second equation, we have
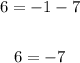
This is false.
Option D:
Through process of elimination, this is the correct answer. However, let's prove it.
We know the first equation worked, so let's try the second:
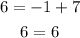
The correct answer is Option D.