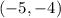Given:

To find:
Rewrite the equation using the completing the square method.
Step-by-step explanation:
It can be written as,
![\begin{gathered} y=3(x^2+10x)+71 \\ =3(x^2+10x+5^2-5^2)+71 \\ y=3[(x^2+10x+5^2)-25]+71 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qghev29hnzvq89urftlmiag91i26mepv68.png)
Using the algebraic identity,
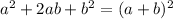
We can write,
![\begin{gathered} y=3[(x+5)^2-25]+71 \\ y=3(x+5)^2-75+71 \\ y=3(x+5)^2-4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/luftnuhlyhhdbo5nabi6m69ec4fohxknik.png)
Therefore, the equation becomes,
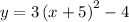
It is of the form,
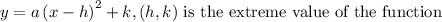
So, the extreme value of the equation is at
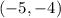
Final answer:
The equation is written as,
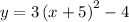
The extreme value of the equation is at