Question

What is the quotient of 2x^3 +3x^2+5x-4 divided by x^2 + x+ 1

Answer 1

`2*x+1+(2*x-5)/(x^2+x+1)`

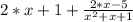
Explanation:

Where, the quotient is 2·x + 1, and the reminder is 2·x - 5

Hence, the above is correct is as follows:

The given dividend is 2·x³ + 3·x² + 5·x - 4

The divisor is x² + x + 1

By long division of a polynomial we have;

2·x + 1 [Quotient]

(2·x³ + 3·x² + 5·x - 4) ÷ (x² + x + 1 )

2·x³ + 2·x² + 2·x

0 + x² + 3·x - 4

x² + x + 1

0 + 2·x - 5

Thurs, we have:

`((2*x^3 + 3*x^2 + 5*x - 4))/(x^2+x+1) =2*x+1+(2*x-5)/(x^2+x+1)`

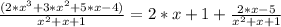
Hence, the correct answer is
`2*x+1+(2*x-5)/(x^2+x+1)`

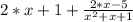
[RevyBreeze]