Question

Select all of the following that can be used to find the height of the tree

Answer 1

Let's draw the scenario to better understand the problem:

The setup appears to form a right triangle. To be able to find the height of the tree, we will be using the Tangent function:

With respect to Θ = 41°,

Adjacent = 53 Feet

Opposite = x

Therefore, the formula for x will be:

`\text{ Tangent }\Theta\text{ = }\frac{\text{ Opposite}}{\text{ Adjacent}}`
`\text{ Tangent }(41^(\circ))\text{ = }\frac{\text{ x}}{\text{ 5}3}`
`\text{ 53Tangent }(41^(\circ))\text{ = x}`

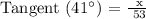
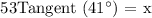
With respect to Θ = 49°,

Adjacent = x

Opposite = 53 Feet

Therefore, the formula for x will be:

`\text{ Tangent }\Theta\text{ = }\frac{\text{ Opposite}}{\text{ Adjacent}}`
`\text{ Tangent }(49^(\circ))\text{ = }\frac{\text{ 5}3}{\text{x}}`
`\text{ x = }\frac{\text{ 5}3}{\text{Tangent }(49^(\circ))}`

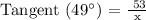
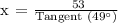
Therefore, the following equations can be used to find the height of the tree:

`\begin{gathered} \text{ 53Tangent }(41^(\circ))\text{ = x} \\ \text{ or} \\ \text{ x = }\frac{\text{ 5}3}{\text{Tangent }(49^(\circ))} \end{gathered}`

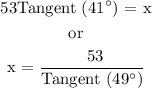
The answer is the 5th and 6th choice.