Let's draw the scenario to better understand the problem:
The setup appears to form a right triangle. To be able to find the height of the tree, we will be using the Tangent function:
With respect to Θ = 41°,
Adjacent = 53 Feet
Opposite = x
Therefore, the formula for x will be:
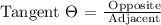
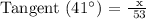
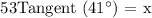
With respect to Θ = 49°,
Adjacent = x
Opposite = 53 Feet
Therefore, the formula for x will be:
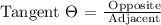
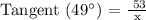
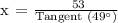
Therefore, the following equations can be used to find the height of the tree:
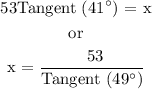
The answer is the 5th and 6th choice.