The total number of students is 400, thus, the universal set is 400
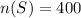
The number of students that prefer Deli Day will be
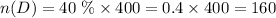
The number of students that prefer Taco Day will be
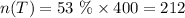
The number of students that prefer Pizza Day will be
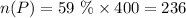
The number of students that prefer all three days will be

The number of students that prefer Pizza Day only will be
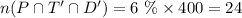
The number of students that prefer Taco Day and Pizza Day will be
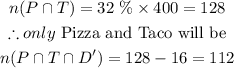
The number of students that prefer Taco Day and Deli Day will be
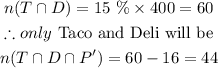
The number of students that prefer Pizza and Deli day only will be
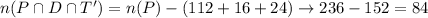
The number of students that prefer Deli Day only will be
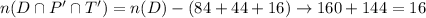
The number of students that prefer Taco Day only will be
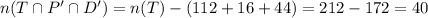
The number of students that preferred none will be
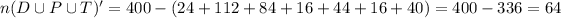
Hence, the Venn diagram is shown below