Question

Write a system of equations to describe the situation below, solve using substitution, and fill in the blanks.Isaac just got his commercial driver's license and is starting a new career as a truck driver. Getting trained and licensed involved a one-time cost of $477. Gas and insurance end up costing him $2 per kilometer. For his first delivery, Isaac will get paid $429 plus $3 per kilometer that he drives. If he drives a certain distance on this delivery, Isaac will break even, making back all the money he had to spend. What distance would he have to drive? How much would both the costs and the earnings be?

Answer 1

Let the total distance covered by Isaac be represented by x.

Given:

cost of getting trained and licensed = $477

cost of insurance and gas for x kilomoter covered = $2x

Total cost =

`\text{\$477 + \$2x ----- equation 1}`

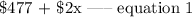
Total earnings for x kilometer covered =

`\text{\$429 +\$3x ---- equation 2}`

Breakeven is the point at which the amount made or earned is equivalent to the amount spent.

For Isaac to break even, his total cost or expenses must be equal to his total earnings.

Thus, Total cost = Total earnings

`477\text{ + 2x }=\text{ 429 + 3x}`

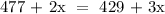
To solve for x, collect like terms

`\begin{gathered} 2x\text{ - 3x = 429 -477} \\ -x\text{ = -48} \\ \end{gathered}`

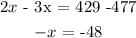
divide both sides by the coefficient of x, which is -1.

thus

`\begin{gathered} (-x)/(-1)\text{ = }\frac{\text{-48}}{-1} \\ \Rightarrow x\text{ =48} \end{gathered}`

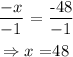
Thus,

Total cost:

`\begin{gathered} 477\text{ + 2x} \\ =477\text{ + 2(48)} \\ =477\text{ +96} \\ =573 \end{gathered}`

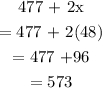
Total earnings:

`\begin{gathered} 429+3x \\ =429\text{ + 3(48)} \\ =429\text{ + 144} \\ =573 \end{gathered}`

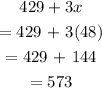
Thus, the total cost is $573 and the total earnings is $573