Question

If this is the right answer I’m bad at math I never understand it

Answer 1

The given triangle is a right-angled triangle

`FE=12\text{units and m}\angle F=35^o\text{.}`
`\text{Here m}\angle E=90^o`

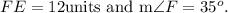
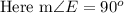
Using the triangle sum property, we get

`m\angle D+m\angle F+m\angle E=180^o_{}`
`\text{ Substitute }\angle mF=35^o\text{ and m}\angle E=90^o,\text{ we get}`

`m\angle D+35^o+90^o=180^o`

`m\angle D+125^o=180^o`

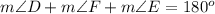
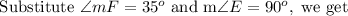
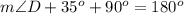
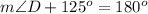
Adding -125 degrees on both sides, we get

`m\angle D+125^o-125^o=180^o-125^o`
`m\angle D=55^o`

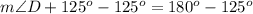
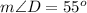
Recall the formula for cosine

`\text{cos}\theta=\frac{Adjacent\text{ side}}{\text{Hypotenuse}}`

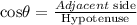
Substitute adjacent side =FE=12 units and Hypotenuse =FD and angle is 35 degree.

`\cos 35^o=(12)/(FD)`

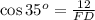
Taking reciprocal and multiplying 12 on both sides.

`(12)/(\cos 35^o)=(FD)/(12)*12`

`FD=(12)/(\cos35^o)`
`\text{Use }\cos 35^o=0.819.`

`FD=(12)/(0.819)=14.65\text{ units }`

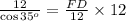
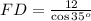
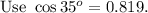
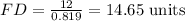
Recall the formula sine.

`\sin \theta=\frac{opposite\text{ side}}{\text{hypotenuse}}`

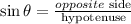
Substitute opposide side=DE and Hypotenuse =FD=14.65 units and angle is 35 degrees.

`\sin 35^o=(DE)/(14.65)`
`Use\sin 35^o=0.573`

`0.573=(DE)/(14.65)`
`DE=0.573*14.65=8.39=8.40`

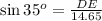
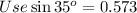
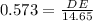
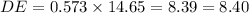
Hence the required answer is

`m\angle D=55^o\text{ , DE=8.40 units and DF=14.65 units.}`

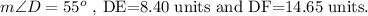
Hence the option B is correct.