The given triangle is a right-angled triangle
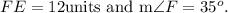
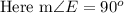
Using the triangle sum property, we get
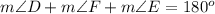
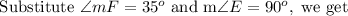
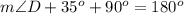
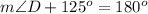
Adding -125 degrees on both sides, we get
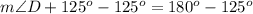
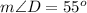
Recall the formula for cosine
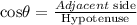
Substitute adjacent side =FE=12 units and Hypotenuse =FD and angle is 35 degree.
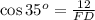
Taking reciprocal and multiplying 12 on both sides.
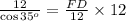
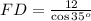
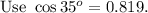
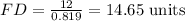
Recall the formula sine.
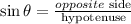
Substitute opposide side=DE and Hypotenuse =FD=14.65 units and angle is 35 degrees.
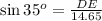
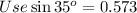
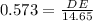
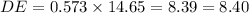
Hence the required answer is
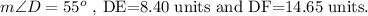
Hence the option B is correct.