Question

A tumor doubles in size every 5 months. If the initial size of the tumor is 6 cells, how many cells will there be in 1 years and in 7 years

Answer 1

The monthly growth rate of the tumor is:

`r=2`

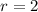
Then, we can formulate the growth model knowing that the initial size is 6 cells, using an exponential model:

`S(t)=S_0\cdot r^(t/5)`

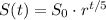
Where S(t) is the size of the tumor at month t, S₀ is the initial size, and r is the growth rate per 5 months. Using the corresponding values:

`S(t)=6\cdot2^(t/5)`

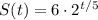
In one year, we have 12 months, so t = 12. Using the model:

`\begin{gathered} S(12)=6\cdot2^(12/5)=31.67 \\ \Rightarrow S(12)=32 \end{gathered}`

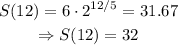
In 7 years, there are 7*12 = 84 months, so t = 84:

`\begin{gathered} S(84)=6\cdot2^(84/5)=684628.82 \\ \Rightarrow S(84)=684629 \end{gathered}`

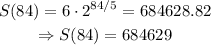
There are 32 cells after 1 year, and 684629 cells after 7 years.