Question

A bullet with a mass of 45 g is fired into a 8.3-kg block of wood resting on a floor against a spring. This ideal spring (k = 76 N/m) has a maximum compression of 28 cm. What was the initial speed of the bullet?

Answer 1

Given data:

* The mass of the bullet is m_1 = 45 g.

* The mass of the block is m_2 = 8.3 kg.

* The spring constant in the given case is k = 76 N/m.

* The maximum compression of the spring is x = 28 cm.

Solution:

According to the law of conservation of energy, the kinetic energy of the block and bullet in the starting state of compress is equal to the potential energy of the maximum compressed spring.

Thus,

`\begin{gathered} (1)/(2)(m_1+m_2)v^2=(1)/(2)kx^2 \\ (m_1+m_2)v^2=kx^2 \end{gathered}`

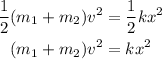
Substituting the known values,

`\begin{gathered} (45*10^(-3)+8.3)* v=76*(28*10^(-2))^2 \\ (0.045+8.3)* v=76*(0.28)^2 \\ 8.345v=5.96 \\ v=(5.96)/(8.345) \end{gathered}`

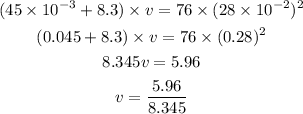
By simplifying,

`v=0.714\text{ m/s}`

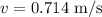
According to the law of conservation of mass,

`m_1u+m_2(0)=(m_1+m_2)v`

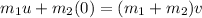
where 0 indicates the rest state of the block in the initial state,

Substituting the known values,