Question

A siren emits a sound at 1700 Hz. Assume the air temperature is 30oC. What frequency would a stationary observer hear if the car with the siren is travelling at:A. 25 m/s towards the observerB. 25 m/s away from the observerC. 140 km/h towards the observer

Answer 1

Given data:

* The actual frequency of the sound is f = 1700 Hz.

* The value of the temperature is T = 30 degrees C.

Solution:

The speed of the sound at the given temperature is,

`v_{}=\text{ 349.1 m/s}`

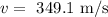
(a). By Doppler's effect, the frequency of the sound heard by the observer is,

`f^(\prime)=f((v)/(v-v_s))`

where v_s is the speed of the source,

Substituting the known values,

`\begin{gathered} f^(\prime)=1700*((349.1)/(349.1-25)) \\ f^(\prime)=1700*((349.1)/(324.1)) \\ f^(\prime)=1831.13\text{ Hz} \end{gathered}`

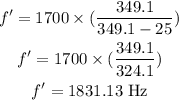
Thus, the frequency of the sound heard by the observer is 1831.13 Hz.

(b). When the car is moving away from the observer, thus, by Doppler's effect, the frequency of the sound heard by the observer is,

`f^(\prime)=f((v)/(v+v_s))`

Substituting the known values,

`\begin{gathered} f^(\prime)=1700*((349.1)/(349.1+25)) \\ f^(\prime)=1700*(349.1)/(374.1) \\ f^(\prime)=1586.4\text{ Hz} \end{gathered}`

Thus, the frequency of the sound heard by the observer is 1586.4 Hz.

(c). The car is moving towards the observer with the speed of,

`\begin{gathered} v_{\text{s}}=140\text{ km/h} \\ v_s=140*(1000)/(60*60) \\ v_s=38.89\text{ m/s} \end{gathered}`

By Doppler's effect, the frequency of the sound heard by the observer is,

`f^(\prime)=f*(v)/(v-v_s)`

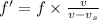
Substituting the known values,

`\begin{gathered} f^(\prime)=1700*(349.1)/(349.1-38.89) \\ f^(\prime)=1700*(349.1)/(310.21) \\ f^(\prime)=1913.12\text{ Hz} \end{gathered}`

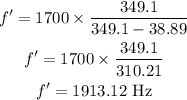
Thus, the frequency of the sound heard by the observer is 1913.12 Hz.