Question

Nathan wants to draw a triangle. He knows that two of the side lenghts are 8 inches and 10 inches.What is a possible lenght for the third side?

Answer 1

hello, to do this exercise, we need to know about the property of the existence of a triangle.

I will call the sides by "a" = 8 inches, "b" = 10 inches and "c" = unknown side

to exist, it has 2 rules:

- the lenght of one side must be less than the sum of the other two sides.

`c<\text{ a + b}`

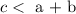
- the third size must be bigger than the absolute value of the difference of the other two sides.

`c\text >`

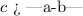
If we put it in one inequation, we have:

`|a-b|\text{ < c < a+b}`

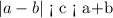
Replacing "a" and "b" with the values we have:

[tex]\begin{gathered} |8-10|\text{ < c < 8+10} \\ |-2|\text{ < c < 18} \\ 2

So, the lenght of the third size can be any value between 2 and 18.

Solution: {3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 18, 19, 20}.