Answer:
• 2.75 astronomical units (AU) in the direction of positive x
,
• 0.265 AU in the direction of positive y
,
• 0.135 AU in the direction of positive z.
Explanation:
First Asteroid
• 2.8 astronomical units (AU) in the direction of positive x
,
• 0.3 AU in the direction of positive y
,
• 0.15 AU in the direction of positive z.
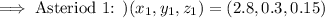
Second Asteroid
The position of the asteroids is given below:
• 2.7 AU in the direction of positive x
,
• 0.23 AU in the direction of positive y
,
• 0.12 AU in the direction of positive z.
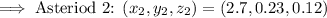
To find the point where they collide, we use the given midpoint formula.
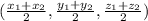
Substitute the values:
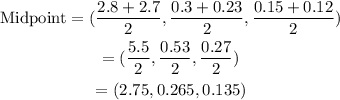
Thus, in this coordinate system, the asteroid will collide at:
• 2.75 astronomical units (AU) in the direction of positive x
,
• 0.265 AU in the direction of positive y
,
• 0.135 AU in the direction of positive z.