Question

The question asks Which lines are Parallel?Line B and Line RLine B and Line GLine R and Line G

Answer 1

Since we are given two points for each line, we will determine which ones are parallel by calculation their slopes, that is:

`m_1=(1-(-4))/(-1-(-4))\Rightarrow m_1=(5)/(3)`

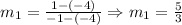
And:

`m_2=(1-(-4))/(2-0)\Rightarrow m_2=(5)/(2)`

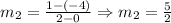
And:

`m_3=(3-(-2))/(5-2)\Rightarrow m_3=(5)/(3)`

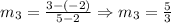
Since we know that two lines are parallel when their slope is the same, we then have that the line to the left and the line to the right are parallel, the line in the middle is not parallel with them.

***

Two lines are perpendicular if you calculate the slope for each line (m1 and m2 respectively) and they follow the next rule:

`m_1=-(1)/(m_2)`

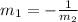
Example:

We have the line:

`y=(1)/(3)x+2`

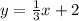
and the line:

`y=-3x+4`

We will determine if they are perpendicular since they are written in the y-intercept form, we can see that the slope of the first line(m1) equals 1/3 and the slope of the second one(m2) equals -3, we then replace the first slope [Or second] in the rule, that is:

`m_1=-(1)/(m_2)\Rightarrow(1)/(3)=-(1)/(m_2)\Rightarrow m_2=-3`

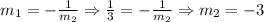
And that way, we determined that they are perpendicular.

***

Example 2.

We have a line(l1) that passes the points (3, 3) and (6, 4) and a line (l2) that passes the points (1, 1) and (2, -2), l1 has a slope of m1 and l2 has a slope of m2.

We determine m1 and m2 using the points, that is:

`m_1=(4-3)/(6-3)\Rightarrow m_1=(1)/(3)`

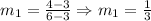
And:

`m_2=(-2-1)/(2-1)\Rightarrow m_2=-3`

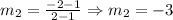
Now, if when we replace m2 in the rule, we get m1, we will have that the lines are perpendicular. Let's remember the rule:

`m_1=-(1)/(m_2)`

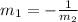
Now, if we replace m2 in the rule, we should get m1 and that would prove that the lines l1 and l2 are perpendicular. But, if we replace m2 and we do not get m1, we will have that the lines are not perpendicular. So, we replace m2 in the rule and we will see if they are perpendicular:

`m_1=-(1)/(m_2)\Rightarrow m_1=-(1)/((-3))\Rightarrow m_1=(1)/(3)`

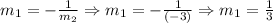
Since we can see that when we replace m2 in the rule we get m1, the lines l1 and l2 are perpendicular.