Given:
The mass of the ball is
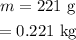
The initial height of the ball is
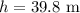
The initial speed of the ball is
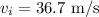
To find:
the impact speed of the ball when it strikes the ground
Step-by-step explanation:
The initial potential energy of the ball is
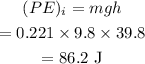
The initial kinetic energy is
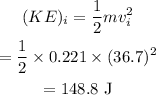
The final energy of the ball is fully kinetic energy. Let the final impact speed of the ball is
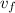
We can write, using the energy conservation principle that
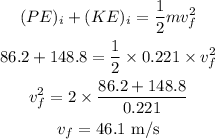
Hence, the final impact speed of the ball is 46.1 m/s.