If the length of the arc traced by such a knot at the bottom of a swinging rope follows a geometric progression, decreasing in this case, the length of each arc will have the following relation:
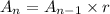
where r stands for the common ratio. We can calculate r and use it to find A6, just as follows:
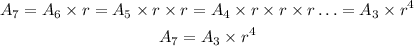
Substituting the values that were given, we can perform the following calculation:
![\begin{gathered} 12=20* r^4\to r=\sqrt[4]{(12)/(20)} \\ r=\sqrt[4]{0.6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/b1jj3ne1j0c5f4qqal19s8x27q0am7f2np.png)
Now we will use it in the following relation:
![\begin{gathered} A_7=A_6* r\to12=A_6*\sqrt[4]{0.6} \\ A_6=\frac{12}{\sqrt[4]{0.6}}=(12)/(0.8801\ldots)\cong13.6 \\ A_6=13.6ft \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rgqh8nhw7kguzr26z8dvozzjs0membozcl.png)