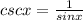Solution:
The question is given below as
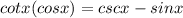
Step 1:
We will make use of the quotient identity below
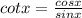
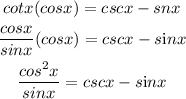
Step 2:
We will make use of the Pythagorean identity below
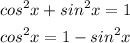
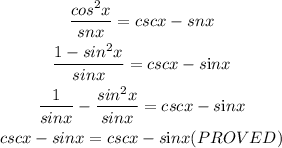
Hence,
STUDENT A and STUDENT B both proved it properly,
STUDENT A proved it from left to right
STUDENT B proved it from right to left
For STUDENT A's work,
Quotient identity was used in step 1
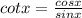
Pythagorean identity was used in step 3
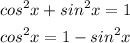
Reciprocal identity was used in step 5