Question

What are the solutions to the system of equations?y=x2−5x−6−x+y=1 (−6, 0) and (0,−1)(−1, 0) and (7, 8)(−1, 0) and (0,−6)(7, 8) and (0,−6)

Answer 1

Given the system of equations:

`\begin{gathered} y=x^2-5x-6\text{ ---- equation 1} \\ -x+y=1\text{ ----- equation 2} \end{gathered}`

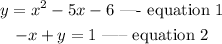
To find the solutions to the system of equations,

step 1: From equation 2, make y the subject of the formula.

Thus,

`\begin{gathered} -x+y=1 \\ \Rightarrow y=1+x\text{ ---- equation 3} \end{gathered}`

step 2: substitute equation 3 into equation 1.

Thus,

`\begin{gathered} \begin{equation*} y=x^2-5x-6 \end{equation*} \\ \Rightarrow1+x=x^2-5x-6 \\ collect\text{ like terms,} \\ x^2-5x-x-6-1=0 \\ \Rightarrow x^2-6x-7=0\text{ ----- equation 4} \end{gathered}`

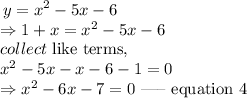
step 3: Solve for x in equation 4.

By factorization,

`\begin{gathered} \begin{equation*} x^2-6x-7=0 \end{equation*} \\ \Rightarrow x^2+x-7x-7=0 \\ x(x+1)-7(x+1)=0 \\ \Rightarrow x-7=0,\text{ or x+1=0} \\ \Rightarrow x=7,\text{ or x = -1} \end{gathered}`

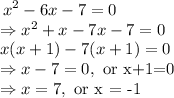
Step 4: Substitute the values of x into equation 3.

Thus, from equation 3

`\begin{gathered} y=1+x \\ when\text{ x=7,} \\ y=1+7 \\ \Rightarrow y=8 \\ when\text{ x= -1} \\ y=1+(-1) \\ \Rightarrow y=0 \end{gathered}`

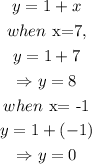
Hence, the solutions to the system of equations are

`(-1,0)\text{ and \lparen7, 8\rparen}`

The second option is the correct answer.