Which of the following are trigonometric identities? Select all that apply

Question

asked Mar 13, 2023 115k views

1 Answer

Chengqi · Answer 1 · 2023-03-20T10:41:08+0000

WSimpe are given the following trigonometric identities:

Part A.

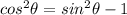
$cos^2\theta=sin^2\theta-1$

This is not a trigonometric identity. The true identity is:

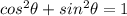
$cos^2\theta+sin^2\theta=1$

Part B

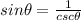
$sin\theta=(1)/(csc\theta)$

This is a trigonometric identity by definition.

Part C.

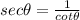
$sec\theta=(1)/(cot\theta)$

This is not a trigonometric identity by definition

Part D.

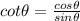
$cot\theta=(cos\theta)/(sin\theta)$

This can be proven to be true if we take the following identity:

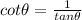
$cot\theta=(1)/(tan\theta)$

Since

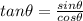
$tan\theta=(sin\theta)/(cos\theta)$

Substituting in the identity for cot we get:

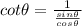
$cot\theta=(1)/((sin\theta)/(cos\theta))$

Simplifying:

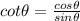
$cot\theta=(cos\theta)/(sin\theta)$

Therefore, the identity is true.

Part W.

$1+cot^2\theta=csc^2\theta$

To prove this identity we will use the following identity:

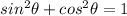
$sin^2\theta+cos^2\theta=1$

Now, we divide both sides by the square of the sine:

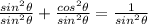
$(sin^2\theta)/(sin^2\theta)+(cos^2\theta)/(sin^2\theta)=(1)/(sin^2\theta)$

The first term is 1:

$1+(cos^(2)\theta)/(s\imaginaryI n^(2)\theta)=(1)/(s\imaginaryI n^(2)\theta)$

We can use the identity in part D for the second term:

$1+cot^2\theta=(1)/(sin^2\theta)$

For the last term, we use identity in part B:

$1+cot^2\theta=csc^2\theta$

Therefore, the identity is true.