Question

I need help on factoring and making it equal to zero

Answer 1

Since the given function is

`f(x)=7x^4-17x^2-12`

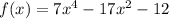
Take 7 as a common factor

`f(x)=7(x^4-(17)/(7)x^2-(12)/(7))`

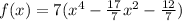
Now let us make the trinomial completing square

Divide the middle term by 2, then square it

`\begin{gathered} ((17)/(7))/(2)x=(17)/(14) \\ ((17)/(14))^2=(289)/(196) \end{gathered}`

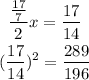
So we will add and subtract this value

`\begin{gathered} x^4-(17)/(7)x-12=x^4-(17)/(7)x^2+(289)/(196)-(289)/(196)-12 \\ =(x^4-(17)/(7)x^2+(289)/(196))-(2641)/(196) \end{gathered}`

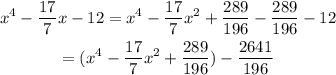
The trinomial is the square of

`(x^4-(17)/(7)x^2+(289)/(196))=(x^2-(17)/(14))^2`

Then the new f(x) is

`f(x)=7\lbrack(x^2-(17)/(14))^2-(2641)/(196)\rbrack`

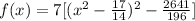
Now we can solve it by equating f(x) by 0

`\begin{gathered} f(x)=0 \\ 7\lbrack(x^2-(17)/(14))^2-(2641)/(196)\rbrack=0 \end{gathered}`

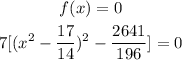
Divide both sides by 7 and add 2641/196 to both sides

`\begin{gathered} (x^2-(17)/(14))^2-(2641)/(196)+(2641)/(196)=0+(2641)/(196) \\ (x^2-(17)/(14))^2=(2641)/(196) \end{gathered}`

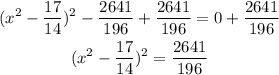
Take a square root to both sides

`(x^2-(17)/(14))=\pm\sqrt[]{(2641)/(196)}`

Add 17/14 to both sides

`\begin{gathered} x^2-(17)/(14)+(17)/(14)=\pm\sqrt[]{(2641)/(196)}+(17)/(14) \\ x^2=\pm4.885047188 \end{gathered}`

We will cancel the -ve value because no square root of -ve values, then

Take a square root for 4.885047188 to find x

`\begin{gathered} x=\pm\sqrt[]{4.885047188} \\ x=\pm2.210214286 \end{gathered}`