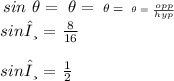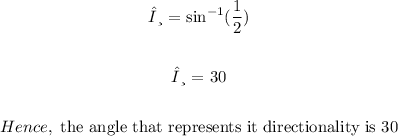Answer:
the angle θ that represents the directionality is 30°
Step-by-step explanation:
Given:
the angle of impact is related to the width w and the length l of the splatter by sinθ = w/l
width = 8 millimeters, length = 16 millimeters
To find:
the angle θ that represents the directionality
We will use the diagram to get the measure of the angle: