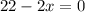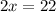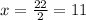Question

PLEASE HELP!PLEASE HELP!d) Use the equation of the volume of the box to find the values of x that make V= 0.

Answer 1

worriAnswer

• a) Expression of height: x inches.

,

• b) Base: , ,22 - 2x, ,inches by 22 - 2x inches.

,

• c) Function of the Volume:

`V=(484x-88x^(2)+4x^(3))`

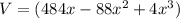
• d) x = 0, 11.

Step-by-step explanation

a)

The figure is not at scale, however, as we can see, the blue square in the image above would be the base of the box. Then, if we fold the corners using that base, then the height of the box is x.

b)

We can also use the image drawn above to see that the base is the blue square. In this case, we have to subtract x from each side as follows:

`=22-x-x`
`=22-2x`

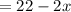
As it is a square, the length of the sides is the same. Then, the base is 22 - 2x inches by 22 - 2x inches.

c)

Using the formula V = lwh where l represents the length, w the width and h the height, we get:

`V=(22-2x)(22-2x)(x)`

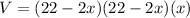
Simplifying we get:

`V=(22-2x)^2(x)`
`V=(484-88x+4x^2)(x)`
`V=(484x-88x^2+4x^3)`

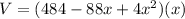
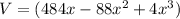
d)

To find these values, it is easier to do it with the factored expression of V, as we can use each factor and set it to 0.

`V=(22-2x)^(2)(x)`

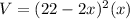
Setting each factor to 0:

`0=(22-2x)^2`
`(x)=0`

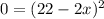
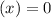
From here, we can see that one of these values is x = 0, the other one is x = 11:

`22-2x=0`
`2x=22`
`x=(22)/(2)=11`