Question

Which pair of functions are inverses of each other?1+6A. f(x) = - 6 and g(x) =B. f(x) = { + 4 and g(x) = 3x - 4C. f(x) = 2x– 9 and g(x) = $49D. f(x) = { and g(x) = 5x3

Answer 1

To know if a pair of functions are inverses of each other we must verify if

`(f\circ g)(x)=(g\circ f)(x)=x`

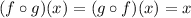
Option A.

`f(x)=(2)/(x)\text{ and }g(x)=(x+6)/(2)`

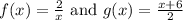
Then

`\begin{gathered} (f\circ g)(x)=f(g(x)) \\ =(2)/((x+6)/(2))=(4)/(x+6) \end{gathered}`

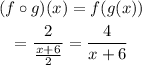
So, option A is not the correct answer.

Option B.

`f(x)=(x)/(3)+4\text{ and}g(x)=3x-4`

Then

`\begin{gathered} (f\circ g)(x)=f(g(x)) \\ =(3x-4)/(3)+4 \\ =x-(4)/(3)+4 \\ =x+(8)/(3) \end{gathered}`

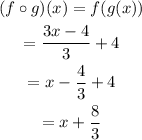
So, option B is not the correct answer.

Option C.

`f(x)=2x-9\text{ and }g(x)=(x+9)/(2)`

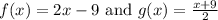
Then

`\begin{gathered} (f\circ g)(x)=f(g(x)) \\ =2((x+9)/(2))-9 \\ =x+9-9 \\ =x \end{gathered}`

And

`\begin{gathered} (g\circ f)(x)=g(f(x)) \\ =(2x-9+9)/(2) \\ =(2x)/(2) \\ =x \end{gathered}`

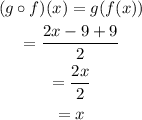
Finally, we can see that option C meets the condition.

So, the answer is letter C.