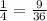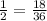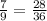In this problem, we want to write equivalent fractions that share a common denominator.
To find the common denominator, we need to find the lowest common multiple of the denominator for each fraction. So, we need to find the LCM (lowest common multiple) for 4, 2, and 9.
One method is to list multiples of each number until you find one that works. My advice is to start with the largest number, as the lists of smaller numbers can get pretty long.
Let's list the first five multiples of 9:
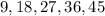
We see that 9 is not a multiple of 2 or 4.
We see that 18 is a multiple of 2 (2 times 9), but not 4.
As we move through the list, we can check the multiples until it works. In this case, 36 is our common multiple:
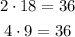
Now we want to rewrite each of our fractions using 36 as our denominator.
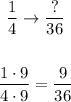
Next, we'll do 1/2:

Finally, we'll find the last fraction for 7/9:
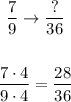
So now we have all our equivalent fractions for 1/4, 1/2, and 7/9.