Question

67. A projectile is fired from a height of 4.5 meters above the ground of a level surface at an initial upwardsvelocity of 30 meters per second. Its height above level ground is given by the equation h=-4.91^2 + 30t + 4.5. After how many seconds, t, will the ball hit the ground. Find using the quadratic formula and round to the nearest tenth of a second.

Answer 1

We have an equation h(t) describing the height of the projectile:

`h(t)=-4.9t^2+30t+4.5`

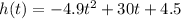
We have to find the time t when it hits the ground.

Mathematically, this means:

`h(t)=0`

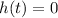
Then, t will be one the roots of the quadratic equation h(t) (NOTE: the other root will be an invalid value of t).

We can calculate the root as:

`\begin{gathered} t=\frac{-30\pm\sqrt[]{30^2-4\cdot(-4.9)\cdot4.5}}{2.\cdot(-4.9)}_{} \\ t=\frac{-30\pm\sqrt[]{900+88.2}}{-9.8} \\ t=\frac{30\pm\sqrt[]{988.2}}{9.8} \\ t\approx(30\pm31.44)/(9.8) \\ t_1\approx(30-31.44)/(9.8)=(-1.44)/(9.8)=-0.15 \\ t_2\approx(30+31.44)/(9.8)=(61.44)/(9.8)=6.27 \end{gathered}`

The root t = -0.15 is not valid, as t has to be greater than 0.

Then, the projectile will hit the ground after t = 6.3 seconds.

Answer: 6.3 seconds.