Question

Determine the ratio of surface area to volume for each prism

Answer 1

Step-by-step explanation

1a. The given prism:

The prism above is a square prism.

The surface area formula of a square prism is:

`\begin{gathered} SA=6l^2 \\ \text{Where:} \\ SA\text{ is the surface area and l is the length of the side of the prism.} \end{gathered}`

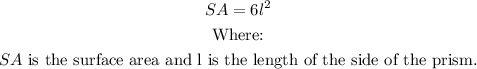
From the given prism, l = 10 cm

Therefore, the surface area will be:

`\begin{gathered} SA=6*(10cm)^2 \\ SA=6*100cm^2 \\ SA=600cm^2 \end{gathered}`

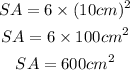
The formula for the volume of a square prism is:

`\begin{gathered} V=l^3 \\ \text{Where:} \\ V\text{ is the volume and l is the length of the prism.} \end{gathered}`

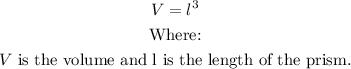
Substitute l = 10 cm:

`\begin{gathered} V=(10cm)^3 \\ V=1000cm^3 \end{gathered}`

The SA = 100 cm² and V = 1000 cm³

So the ratio of the surface area, SA, to volume, V, is:

`\begin{gathered} SA\colon V=600\colon1000 \\ To\text{ the lowest ratio;} \\ SA\colon V=3\colon5 \end{gathered}`

Hence, the ratio of the surface area, SA, to volume, V, of the prism is 3:5

1b. The given prism:

The prism is a rectangular prism.

The surface area, SA, formula of a rectangular prism is:

`\begin{gathered} SA=2(lw+lh+wh) \\ \text{Where:} \\ l\text{ is the length,} \\ w\text{ is the width, and} \\ h\text{ is the height} \end{gathered}`

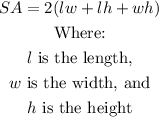
from the figure, l = 6.2 m, w = 4 m, and h = 2 m.

Substitute these values into the formula to get the surface area, SA:

`\begin{gathered} SA=2(6.2*4+6.2*2+4*2) \\ SA=2(24.8+12.4+8) \\ SA=2(45.2) \\ SA=90.4m^2 \end{gathered}`

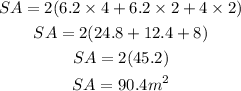
The formula for the volume, V, of a rectangular prism is:

`V=lwh`

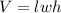
Substitute l = 6.2m, w = 4 m and h = 2 m into the formula to find V:

`\begin{gathered} V=6.2m*4m*2m \\ V=49.6m^3 \end{gathered}`

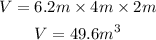
The SA = 90.4 m² and V = 49.6 m³

So the ratio of the surface area, SA, to volume, V, of the rectangular prism is:

`\begin{gathered} SA\colon V=90.4\colon49.6 \\ Convert\text{ the ratio to fraction, we have:} \\ =(904)/(496) \\ T\text{o the lowest fraction,} \\ =(113)/(62) \\ \therefore SA\colon V=113\colon62 \end{gathered}`

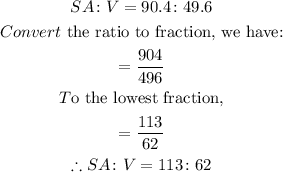
Hence, the ratio of the surface area, SA, to volume, V, of the prism is 113:62