1) Since the points are: A(1, 0), B(13,5), and C(13, 0)
a) To find the length of each leg
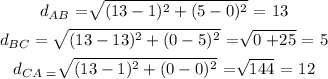
b) Show that these satisfy to the Pythagorean Theorem
Note, a triangle 5,12,13 is a classic Pythagorean triangle, but let's prove it.
This identity must be true on both sides, to prove it. Let's pick the greater side, the hypotenuse = 13 plug it and the other legs as well:
a² =b²+c²
13² = 5²+12²
169 = 25 +144
169 = 169 True