Question

Part 2: Use a sequence to represent the depreciation of a bike. Performance bicycles can cost more than $10,000. Owners of these bikes need to understand the insurance for an investment of this size. The insurance policies often include a rate of depreciation depending on the length of ownership. Depreciation is a percentage deducted from the purchase price because the bike has lost value over time. 1. The table shows a portion of one insurance company’s rate of depreciation for bicycles, which includes the length of ownership and the depreciation factor. This factor is used for an entire year and is multiplied by the original value of the property. OwnershipNot exceeding 1 yearExceeding 1 year but not exceeding 2 yearsExceeding 2 years but not exceeding 3 yearsExceeding 3 years but not exceeding 4 yearsDepreciation Factor8%12%18%27% a) What type of sequence can be used to represent the depreciation factor of the bike over time? Explain. (2 points) b) Write the formula for the nth term in the sequence. (2 points) c) A bike has a purchase price of $8,990. Using the sequence for the rate of depreciation, what is the insurance value of the bike in the fourth year of ownership? (2 points) 2. For the following steps, consider the series that represents the sum of the terms in the sequence for the depreciation factor of the bike over time. a) Write a formula for the sum of the first “n” terms in the sequence representing the depreciation factors. (2 points) b) What does the series represent to the bike owner? (3 points) c) Is the series helpful to the bike owner? Explain why or why not. (3 points)2. For the following steps, consider the series that represents the sum of the terms in the sequence for the depreciation factor of the bike over time. a) Write a formula for the sum of the first “n” terms in the sequence representing the depreciation factors. (2 points)b) What does the series represent to the bike owner? (3 points)c) Is the series helpful to the bike owner? Explain why or why not. (3 points)

Answer 1

The depreciation factor follows the sequence below:

8%, 12%, 18%, 27%

The difference between consecutive values are +4, +6, +9

The second differences are +2, +3. They are not equal, so the sequence is not quadratic.

To find out if this is a geometric sequence, we divide consecutive terms as follows:

`\begin{gathered} (12)/(8)=1.5 \\ (18)/(12)=1.5 \\ (27)/(18)=1.5 \end{gathered}`

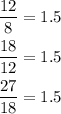
Since all of these ratios are equal, this is a geometric sequence with a common ratio of r = 1.5 (or 3/2).

b)

The formula for the n-th term of a geometric sequence is:

`a_n=a_1\cdot r^(n-1)`

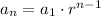
Where a1 is the first term. Substituting:

`a_n=8\cdot\mleft((3)/(2)\mright)^(n-1)`

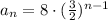
c) It can be helpful to the bike owner because if he/she owns a bike for more than 4 years, they could estimate the depreciation % even if it's not present in the table.

For example, if the length of the ownership is n = 6 years, the depreciation factor is:

`\begin{gathered} a_6=8\cdot\mleft((3)/(2)\mright)^(6-1) \\ a_6=8\cdot(1.5)^5 \\ a_6=60.75 \end{gathered}`

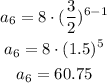
The bike is depreciated by 60.75%

2)

a)

The sum of the terms is:

8% + 12% + 18% + 27% + 40.5% + 60.75% + ...

The last two terms were obtained with the formula.

The sum of n=1 is S1 = 8

The sum of n=2 is S2 = 20

The sum of n=3 is S3 = 38

The sum of n=4 is S4 = 65

The sum of the n first terms of a geometric series is:

`S_n=a_1\cdot(r^n-1)/(r-1)`

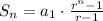
Substituting a1 = 8, r = 1.5:

`\begin{gathered} S_n=8\cdot(1.5^n-1)/(1.5-1) \\ S_n=8\cdot(1.5^n-1)/(0.5) \\ S_n=16\cdot(1.5^n-1) \end{gathered}`

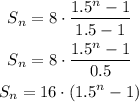
b) For the bike owner, the series represent the cumulative depreciation factor after n years of ownership.

c) I don't see why it could be helpful to the bike owner because the depreciation factor is not cumulative. He/she won't matter for the sum of the factors.