Answer:
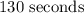
Step-by-step explanation:
Here, we want to get the time a swimmer must complete the backstroke, in order to be considered for a scholarship
What we need to find here is the time in which the probability would be less than 6% (or 6/100 = 0.06)
Now, let us get the z-score to the right of 0.06 but closest to it
By using the normal distribution table, we have this value as:

Recall, mathematically:
![z-score\text{ = }\frac{x-\operatorname{mean}}{SD}]()
Substituting the values, we have it that:
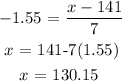
The value of x can be approximated as 130 seconds