Question

Find the inverse function of -|x-1|-2Also find the domain and range of f and the f inverse in interval notation

Answer 1

To find the inverse function of y = -|x-1|-2, we first need to switch the variables y and x:

x = -|y-1|-2

Then, we need to isolate the variable y again:

`\begin{gathered} x=-|y-1|-2 \\ x+2=-|y-1| \\ |y-1|=-x-2 \\ \left\{ \begin{aligned}y-1=-x-2,\text{ if y-1}\ge\text{0} \\ y-1=-(-x-2),\text{ if y-1<0}\end{aligned}\right. \\ \left\{ \begin{aligned}y=-x-1,\text{if y}\ge1 \\ y=x+3,\text{ if y<}1\end{aligned}\right. \end{gathered}`

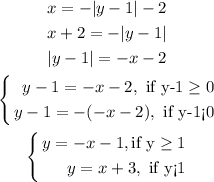
The domain of the function f(x) = -|x-1|-2 is all real numbers, because for any real value of x, we will have a real value for f(x). The interval is (-∞, ∞)

To find the range of f(x), we need to know that the term |x-1| is always positive, because of the module operator. So the smaller value this term can