Question

Y varies directly as x. y=120 when x=8. Find y when x=13

Answer 1

If y varies directly as x, then they have a proportional relationship that can be written as:

`y=k\cdot x`

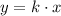
where k is a constant.

We know that, when x = 8, y = 120.

We can find the value of k, but as we only need to find the value of y when x = 13, we wil use a property of proportional relationships:

`k=(y_1)/(x_1)=(y_2)/(x_2)`

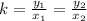
This property tells us that the ratio y/x is constant for all pairs (x,y). Then, we can write:

`\begin{gathered} (x_1,y_1)=(8,120) \\ (x_2,y_2)=(13,y) \end{gathered}`

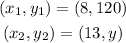
Then, we can write the ratios as:

`\begin{gathered} (y_1)/(x_1)=(y_2)/(x_2) \\ (y)/(13)=(120)/(8) \\ y=(120)/(8)\cdot13 \\ y=15\cdot13 \\ y=195 \end{gathered}`

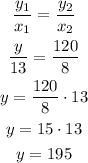
NOTE: that we inplicitly calculated the value of k, that is k = 15. Then we know that the relation is y = 15x.

Answer: y = 195 when x = 13.