From a random sample of 250 gamers with an anual income of $50000, it was obtained that the average gamer spends $206/year on games with a standard deviation of $12.
Sample 1
n₁=250
X[bar]₁=$206
S₁=$12
Another company took a random sample of 225 gamers with an anual income of $50000 and it was obtained that they spend on average $250/year and a standard deviation of $15
Sample 2
n₂=225
X[bar]₂=$250
S₂=$15
A. size of the sample
The greater the sample, the more accurate are the estimations you can make. The sample size of the first sample is greater than the size of the second sample. If you look only at this fact, the first sample should be more accurate.
B. size of the confidence intervals
Confidence intervals with smaller amplitude are considered to be more accurate than those with a greater amplitude. If you look at the formula for the margin of error of a confidence interval for the population mean, you'll notice that the sample size and the margin of error have an inverse relationship, this means that the greater the sample size, the smaller the margin of error and thus, the amplitude of the interval will be smaller
![\downarrow d=Z_{\mleft\lbrace1-(\alpha)/(2)\mright\rbrace}\cdot\frac{S}{\sqrt[]{n}\uparrow}](https://img.qammunity.org/2023/formulas/mathematics/college/8by4yuy7jo7yutkzkoykn58eafcvrl87k1.png)
Since
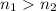
The amplitude of the interval for the first sample is expected to be smaller than the amplitude of the inverval for the second sample, so the CI for the first sample will be more accurate.
C. reliability of the data
The first video games company took the word of the gamers as true while the second company verified that they weren't lying about their annual income.
The information obtained by the second company is more reliable than the information obtained by the first company.
D. randomization
The text states that both companies took "random samples" so the randomization condition checks for both samples.
The reason why the second sample is more believable than the first one is because the data on the second sample was verified. Option C