Question

A loan of S36,000 is made at 7.75% Interest, compounded annually. After how many years will the amount due reach S65,000 or more?

Answer 1

Compound interest formula:

`A=P(1+(r)/(n))\placeholder{⬚}^(nt)`

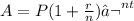
A is the amount after t years

P is the principal

r is the interest rate in decimals

n is the number of times interest is compound

t is the time in years

For the given situation:

A=65,000

P=36,000

r=0.0775

n=1

t=t

`65,000=36,000(1+(0.0775)/(1))\placeholder{⬚}^(1*t)`

Solve the equation for t:

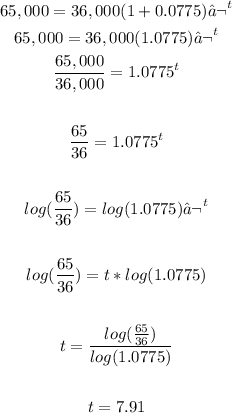
`\begin{gathered} 65,000=36,000(1+0.0775)\placeholder{⬚}^t \\ 65,000=36,000(1.0775)\placeholder{⬚}^t \\ (65,000)/(36,000)=1.0775^t \\ \\ (65)/(36)=1.0775^t \\ \\ log((65)/(36))=log(1.0775)\placeholder{⬚}^t \\ \\ log((65)/(36))=t*log(1.0775) \\ \\ t=(log((65)/(36)))/(log(1.0775)) \\ \\ t=7.91 \end{gathered}`Then, after approximately 8 years the amount due will reach $65,000 or more