Compound interest formula:
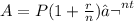
A is the amount after t years
P is the principal
r is the interest rate in decimals
n is the number of times interest is compound
t is the time in years
For the given situation:
A=65,000
P=36,000
r=0.0775
n=1
t=t
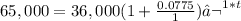
Solve the equation for t:
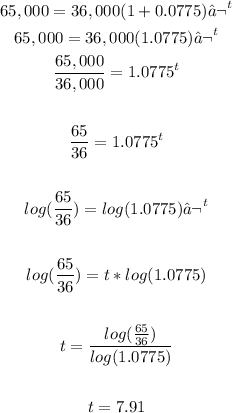
Then, after approximately 8 years the amount due will reach $65,000 or more