Question

Angelo the alligator is laying out next to a perfectly circular pond. He is 36 feet from the edge of the pond and 48 feet from the point of tangency. Determine the radius of the pond

Answer 1

We can see from the question, that we have the following triangle:

We can see that we have a right triangle, and two sides of it. The side with a measure of 48 is tangent to the circle, so it forms a right angle with the circle, and we can see that one of the sides is the radius of the pond.

Then, we can use the Pythagorean Theorem to find the radius of the pond as follows:

`r^2+48^2=(36+r)^2`

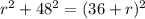
We have that the sum of the square of the length of one side, r, and the square of the length of the other side is equal to the square of the hypotenuse (the largest side of a right triangle, which is 36 + radius of the circle). Then, we need to solve the equation for r, as follows:

`r^2+48^2=36^2+2\cdot36\cdot r+r^2`
`r^2+2304^{}=1296+72r+r^2`

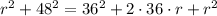
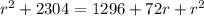
Then, we have:

1. Subtract r^2 to both sides of the equation:

`r^2-r^2_{_{}}+2304=1296+72r+r^2_{}-r^2`
`2304=1296+72r`

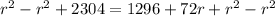
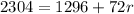
2. Subtract 1296 to both sides of the equation:

`2304-1296=1296-1296+72r\Rightarrow_{}1008=72r`

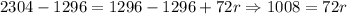
3. Divide by 72 to both sides of the equation:

`(1008)/(72)=(72r)/(72)\Rightarrow r=(1008)/(72)\Rightarrow r=14`

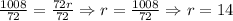
Therefore, the radius of the pond is 14 ft.